NextRoll

HyperLogLog and MinHash

Written by Andrew Pascoe, July 10, 2013

At AdRoll, we have a lot of data to deal with. As we keep accumulating all of this data, our scaling issues become more complicated, and even something as simple as counting becomes a bit of a chore. After using Bloom filters to count uniques, we eventually wanted to find something more space efficient.

We started researching, and implemented a form of HyperLogLog, which gives us the ability count uniques with good accuracy, do it in a distributed way, and keep our memory and storage requirements down. One of the drawbacks though, was that we couldn’t take intersections with these structures, and so we tacked on the additional structure of MinHash.

This blog post briefly covers our research. For the full, gory mathematical details, I also wrote a much more thorough, yet casual, paper, with way more graphs and analysis. If that’s what you’re looking for, go straight to the paper: there’s nothing in the blog post that isn’t covered in the paper.

HyperLogLog++

The first stop we made was the Google paper “HyperLogLog in Practice: Algorithmic Engineering of a State of The Art Cardinality Estimation Algorithm” by Heule, Nunkesser, and Hall. It describes some improvements to the HyperLogLog algorithm, which the authors now call HyperLogLog++. Double double.

Essentially, it works like this: When you go to add an element to the structure, you hash it into 64 bits. From there, you divide up the hash as:

$$\overbrace{101\ldots 011}^{p\ \rm{bits}}\overbrace{001\ldots 110}^{64 - p\ \rm{bits}}$$

Where \(p\) is your defined precision. The first chunk defines the index \(i\) into an array \(M\) which has \(2^p\) bins, all initialized to zero. Now, for the second chunk, count the number of leading zeros plus one (in this case, three), which we’ll call \(z\). Then you set \(M[i] = \max\left\{M[i], z\right\}\). By the end, you have a bunch of bins with a bunch of numbers in them. Now what?

Well, it turns out that you can get an estimate of how many unique elements were added to this structure. And the way you do this is:

$$E = 2^{2p} \left(2^p \int_{0}^{\infty} \left( \log_2 \left( \frac{2 + u}{1 + u} \right) \right)^{2^p} {\rm{d}}u\right)^{-1} \left( \sum_{i=0}^{2^p - 1} 2^{-M[i]} \right)^{-1}$$

Pretty nasty, but that second term converges. The Google paper recommends:

$$\begin{matrix} p & & \rm{second\ term} \\ 4 & & 0.673 \\ 5 & & 0.697 \\ 6 & & 0.709 \\ > 7 & & 0.7213/(1 + 1.079/2^p) \end{matrix}$$

And we’re still not done. If there are any zeros left in \(M\), we count them (call it \(V\)) and output \(E = 2^p \log\left(\frac{2^p}{V}\right)\). And if \(E < 5 \cdot 2^p\), then we go through a bias correction step; the Google paper has an addendum of empirically derived values for this. Otherwise, we can just output \(E\).

The Google paper has some other enhancements as well, such as a sparse representation, but that’s beyond the scope of this blog post. Anyway, this turns out to work pretty well. Here’s a graph of relative errors up to a cardinality of 200 million, run 128 times for each cardinality tested, for \(p = 18\) with \(3\sigma\) ranges overlaid:

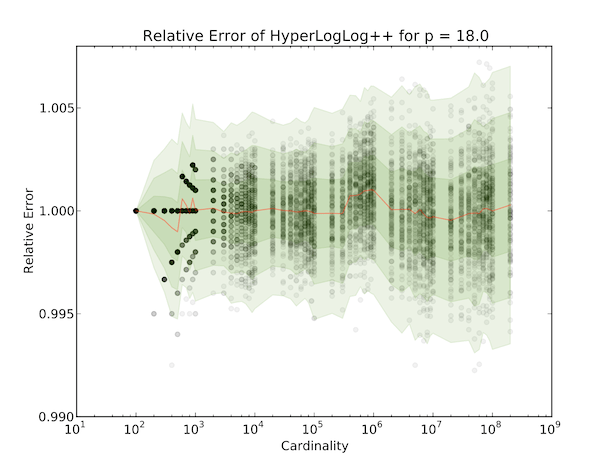
One of the really nice things about these HyperLogLog structures is that you can get unions for free; with two such structures, \(M_1\) and \(M_2\), you just need \(M[i] = \max\left\{M_1[i], M_2[i]\right\}\). This means that we can tally up uniques in a distributed computing environment. It’s also possible to reduce the precision of a HyperLogLog structure if you need to union two of them that have different array sizes, but you can check out the full paper for those details.

Intersections are a different story. Some other blogs suggest using the inclusion-exclusion principle, but this can get somewhat unwieldy, and potentially give some wild results. At AdRoll, we decided that we were willing to sacrifice some space efficiency by effectively tacking on a completely separate structure.

MinHash

MinHash is an algorithm that computes an estimate of something called the Jaccard Index, which is defined as:

$$J(A,B) = \frac{|A \cap B|}{|A \cup B|}$$

It functions as a measure of how similar two sets are. But let’s abandon this notion of similarity, and extend the metric, so that we can talk about interesecting lots of sets:

$$J(A_1, A_2,\ldots,A_n) = \frac{\left|\bigcap_{i=1}^{n}A_i\right|}{\left|\bigcup_{i=1}^{n}A_i\right|}$$

The variant of MinHash that we’ll be using employs only one hash function, \(h(\cdot)\), and for each input set, we keep the \(k\) lowest values after going through this hash function (I’ll be using the notation \(\min_k\) to represent this, which overloads its usual mathematical meaning). If our hash function is uniformly distributed and is not prone to collisions, we can say that:

$$\min_k\left\{\bigcup\min_k\left\{h\left(A_i\right)\right\}\right\} = \min_k\left\{h\left(\bigcup A_i\right)\right\}$$

is a random sample of our total space. That means that we can check each element in this sample, and see if it is in every \(\min_k\left\{h\left(A_i\right)\right\}\). By tallying up all the elements that satisfy this criterion (call it \(y\)), we can say:

$$\frac{y}{k} \approx J(A_1,\ldots,A_n)$$

Now that we have this estimate, we know that:

$$\left|\bigcap A_i \right| = J(A_1,\ldots,A_n)\cdot\left|\bigcup A_i\right| \approx \rm{MinHash\ Result} \cdot \rm{HLL\ Result}$$

Hey, we’re hashing all this stuff with HyperLogLog++ anyway, right? We tested this assertion with a HyperLogLog++ structure of \(p = 18\) and a MinHash \(k = 98304\), which in our implementation adds up to a 1MB structure. We took two randomly generated sets, each with 100 million elements, and then intersected them for a variety of Jaccard Indices, repeating the process 128 times. This is the result:

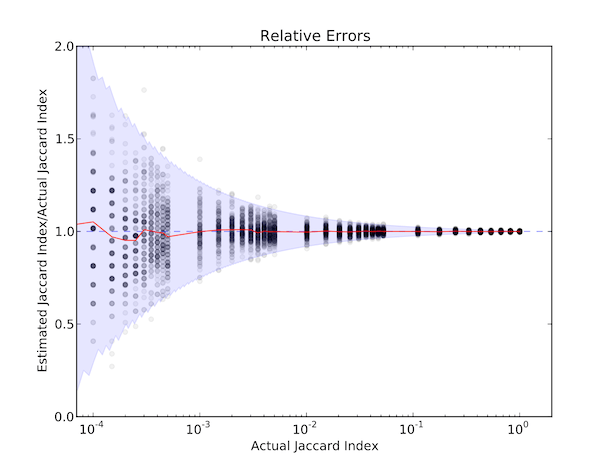
The blue region represents our theoretical 99% confidence bounds (you can read about the theory in the paper, along with how to pick a good \(k\) for your own purposes), and we see that our experimental results corroborate our predictions well. You can see that the more the sets overlap, the better we are at predicting the size of that overlap. However, even for small intersections, we do pretty well: we can be 99% sure that if the overlap is 0.01%, we’ll report that between 0.00% and 0.02%, which is quite reasonable. A 1% overlap is 99% likely to be reported between 0.9195% 1.0824%.

Conclusion

If you’re already using HyperLogLog structures in your work, but have been longing for a means of intersecting them, it’s worth checking out out extending your code with a MinHash implementation. While it does require extra processing power to deal with collecting all the minima, it’s possible to get satisfactory performance out of the structure for a relatively low storage or memory footprint.

Last, as a final plug, I get to tackle interesting problems like this all the time throughout the course of my work. If this type of stuff fires you up, AdRoll is hiring, and we would love to hear from you.