Interested in working with us? We are hiring!

See open positions

MaskedLARK Explainer

Chris Evans Written by Chris Evans, August 03, 2021

Background

MaskedLARK is the latest in a number of proposals for Google’s Privacy Sandbox initiative. This initiative aims to increase user privacy in the browser by removing third-party cookies while still preserving the ad-tech ecosystem that has evolved on top of those cookies.

A key part of the current ecosystem are machine learning models, which determine how valuable a given ad is to be shown to a given user: Third-party cookies are used to track to whom ads are shown and whether these ads were effective. This data is then used to train machine learning models to better allocate future advertising dollars.

Privacy advocates don’t want private companies to be able to track the individual history of users, while ad-tech companies want to efficiently spend advertising dollars with effective machine learning models. MaskedLARK provides a compromise: The machine learning models can be trained on individual user data, but neither the ad-tech companies nor any other third party will have access to this raw data. This post will go over the details using one of our NextRoll machine learning models as an example.

The Problem and Solution

The gold standard of ad-tech metrics today is Click-Through-Conversions. A Click-Through-Conversion occurs when a user clicks on an ad and then goes on to “convert” (purchase from the advertiser) within a given time span (usually 30 days). This metric is popular with advertisers as the conversion represents an actual sale while the click shows that the ad influenced the user and led to the conversion. In fact, the Click-Through-Conversion metric is so popular that most browsers promise to continue supporting it even in the absence of third-party cookies. To optimize Click-Through-Conversions, at NextRoll we train a model for P(Convert | Click), the probability that a user converts given that they clicked on an ad.

The training data for this model consists of rows where each row represents a click and has a positive or negative label depending on whether that user went on to convert (Our actual model is a bit more complicated and uses survival models but I’ll ignore that in this post for simplicity).

When a user clicks an ad we log a “click event” and when a user converts with one of our advertisers we log a “conversion event”. Since both of these events have access to and log the third party cookie, we can join the click and conversion events on the third party cookie to build a timeline of the user’s ad interactions and purchases to build our training data:

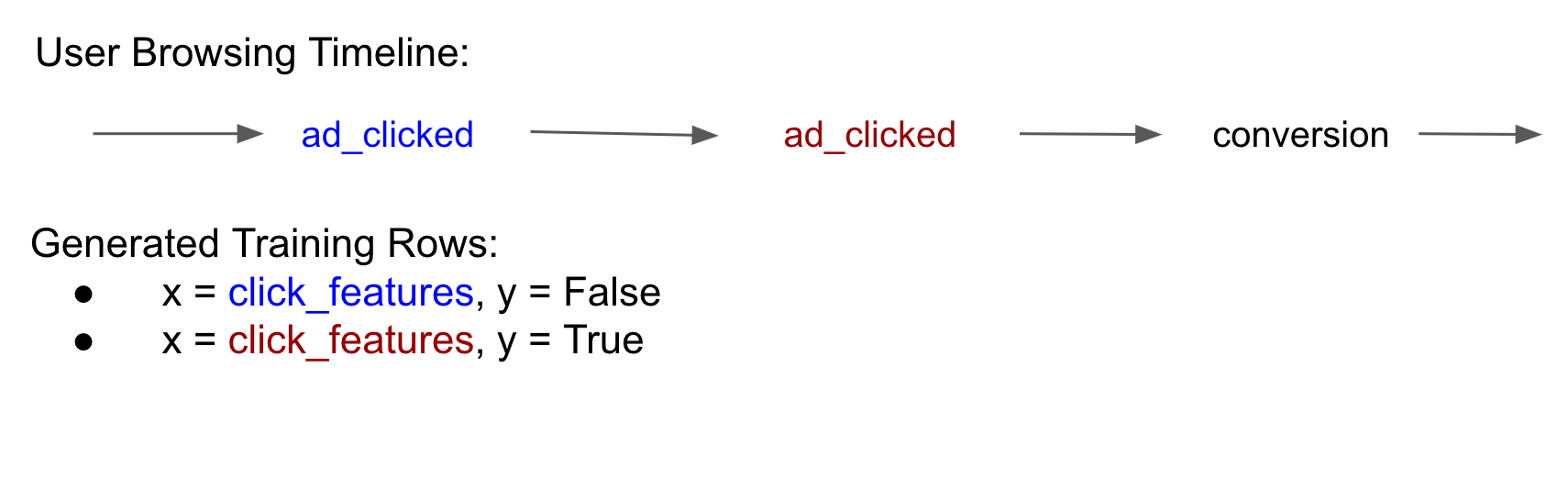
User Browsing Timeline

The MaskedLARK proposal creates this same training set but keeps it within the browser to ensure privacy. Then “helpers” (trusted third parties) perform the computations needed to update our model. We are able to train the model we need while never having access to the raw user data!

But now won’t the helpers have access to the data? To solve this, MaskedLARK proposes a protocol using secret sharing masks where data is split among multiple helpers such that no individual helper can recover the raw data yet their combined computations still produce the desired model update. This will be explained in more detail below but at a high level the flow of MaskedLARK is as follows:

  1. We tell the browser which features x we care about.
  2. The browser keeps track of which ads the user clicks on and whether the user converts. It thereby creates the training data (x, y) for our model – one row for each click with features x and label y determined by whether the user goes on to convert or not.
  3. Using secret sharing masks, the browser splits this training data into H chunks, one for each of H helpers.
  4. Each helper computes the model update over the training data (x, y) it receieves.
  5. We receive the H computations and combine them into a single computed model update with which we update our model.

How Secret Sharing Masks Work

Let’s take a brief detour to understand the idea behind secrete sharing via masks.

Suppose I have a secret number, say 17, and a collection of numbers which sum to 1, say -4, 2, and 3. We will call these numbers “masks”. Suppose now I give each of three “helpers” the secret number multiplied by one of the masks. That is,

Then none of the three helpers knows my secret number and yet if these three numbers are added together they recover my secret number 17! Thus a collection of masks that sum_to_1 can be used to split a secret into pieces such that no party knows the secret and yet the secret can be recovered from the pieces.

Suppose now I take a different number, say 13, and a collection of “masks” which sum to 0, say -5, 2, and 3. Again I give each helper the number multiplied by the corresponding mask. That is,

Now if we add these three numbers we get 0. And so a collection of masks that sum_to_0 can be used to create data that vanishes when combined together.

Finally, we can use both these strategies to not only hide secret numbers but also how many secret numbers there even are: Suppose we have some secret numbers – say just one, 17. We can create some fake numbers – say just one, 13 – and pass to each helper the masked numbers using sum_to_1 masks for the secret numbers and sum_to_0 masks for the fake numbers. Continuing the example above and shuffling the passed data we could have e.g. that

Now each helper doesn’t know how many real secret numbers there are or even whether each number they receive corresponds to a real or fake secret number. And yet when all of these numbers are added together we get -68 + 65 + 26 + 34 + 51 + 39 = 17. That is we are still able to recover the sum of all the true secret numbers!

Back to MaskedLARK

With the idea of masks in mind, let’s return to MaskedLARK. After step 2. the browser has the true training data (x_i, y_i) and to update our model we need to compute

sum(G(x_i, y_i) for (x_i, y_i) in true_data)

where G is the gradient for the loss function for our model (c.f. gradient descent).

For each true data point (x_i, y_i), the browser concocts a number of fake data points. Then for each true data point, it computes a collection of masks that sum_to_1, while for each fake data point, it computes a collection of masks that sum_to_0. It then prepares for each helper a shuffled collection of data [(x_i, y_i, mask)] which is a mix of true and fake data points.

Each helper h receives its share of data and computes

sum(mask * G(x_i, y_i) for (x_i, y_i, mask)
  in mixed_data_for_helper_h)

Finally we (the Ad Server) receieve each of these H computations, and sum them to recover the full model update! This works because the fake data masked with sum_to_0 masks drop out while the true data masked with sum_to_1 combine back into the original data. In mathematical terms,

sum(sum(mask * G(x_i, y_i) for (x_i, y_i, mask)
    in mixed_data_for_helper_h) for h in helpers)
  == sum(G(x_i, y_i) for (x_i, y_i) in true_data)
  == desired gradient computation

As the raw history of the cookie is only contained in the browser, and each helper only gets masked information (including fake data), neither the helpers nor the Ad Server (NextRoll) get access to the user’s private browsing history. And yet, we still get the full power of a machine learning model trained on individual browsing history to allocate future advertising spend.

Extensions

The preceding sections explain the core idea of MaskedLARK in the context of computing a gradient update for a machine learning model. But the same framework could be used to calculate any aggregated quantity over individual user browsing histories. For example, we could compute “the total predicted number of conversions in California” and compare that to “the actual number of conversions in California” to see if our machine learning models are well-calibrated for California. The only limitation is that the computed quantity exhibit the desired interaction with the masks: fake data drops out, and the true data is recovered (this is expressed as a bilinearity condition in this section of the official README)

The MaskedLARK framework can also be augmented with additional privacy-preserving measures such as adding noise to the helpers’ aggregated quantities or using k-anonymity

Conclusion

NextRoll Engineering has been an active participant in the privacy sandbox meetings, which will transform the ad-tech ecosystem in the near future. By keeping at the forefront, we ensure that our machine learning models and systems will continue to be first in class, no matter which proposals are ultimately adopted. If working with large-scale real-time machine learning systems in an evolving environment catches your interest, be sure to check out our careers page.