The Winner's Curse
Introduction
Anytime you have an auction, you have the potential for the winner’s curse, a simple, yet surprising, statistical phenomenon. Despite its simplicity, the effect can have significant financial implications for anyone participating in auctions.
We care about the winner’s curse at NextRoll because we participate in about 100,000 ad auctions per second. In this post, we explain the curse and explore the way it manifests itself in our ad-buying systems.
Understanding the Curse
Let’s pretend Alice is auctioning off a jar containing exactly $25 of spare change she has collected. \(N\) of Alice’s friends participate in the auction, hoping to purchase Alice’s jar of change. No one can open the jar before the auction, but each of Alice’s friends can inspect the jar to estimate the total worth of the coins contained within. After completing their valuations, each of Alice’s friends submit a bid.
Alice’s friends assume one of them can make a few dollars here. However, it may be the case that one of them overestimates the value of the coins in the jar. As a result, that person may bid too much into Alice’s auction. If this happens, that person may, depending on the auction dynamics and the other bids, end up paying Alice more for the jar than the value of the coins contained within.
It turns out that the winner of Alice’s auction will end up overpaying for the jar of change much more frequently than we would naively expect; this is the winner’s curse. To see how this works, let’s denote Alice’s \(i\)th friend’s valuation as follows: where \(\epsilon_i\) is the error each friend makes in their valuation. The highest valuation of the jar of coins among Alice’s \(N\) friends will be:
This highest valuation is very likely to be larger than $25. To see why, let’s assume Alice’s friends are equally likely to overestimate the value of the coins as they are to underestimate it. In this case, for the highest valuation to be less than $25, all \(N\) of Alice’s friend’s bids have to underestimate the value of the jar of coins. This happens only \(\frac{1}{2^N}\) of the time.
This discussion of the highest valuation is important because, typically, the person with the highest valuation will win the auction. Let’s call this person with the highest valuation, whom we expect to win the auction, Bob. If Bob wins the jar of change and tallies up the money, he is probably in for a nasty surprise. Almost every time, the jar will have less money than he anticipated it having. Many times, this effect is so pronounced that not only will Bob have not made as much profit as he had anticipated, he will have lost money! Just like that, Bob has fallen victim to the curse!
Simulating the Curse
To further illustrate this effect, we can make some concrete assumptions and run a simulation. Let’s pretend the error each of Alice’s friends make when estimating the jar of coins’ value is distributed normally with a mean of $0 and a standard deviation of $3. That is, \(\epsilon_i \sim \mathcal{N}(0, 3^2)\). Let’s pretend Alice is running a second-price auction, in which the bidders naively assume bidding their noisy valuation is optimal. Below we see what happens with 4, 7, and 10 of Alice’s friends bidding into her auction.
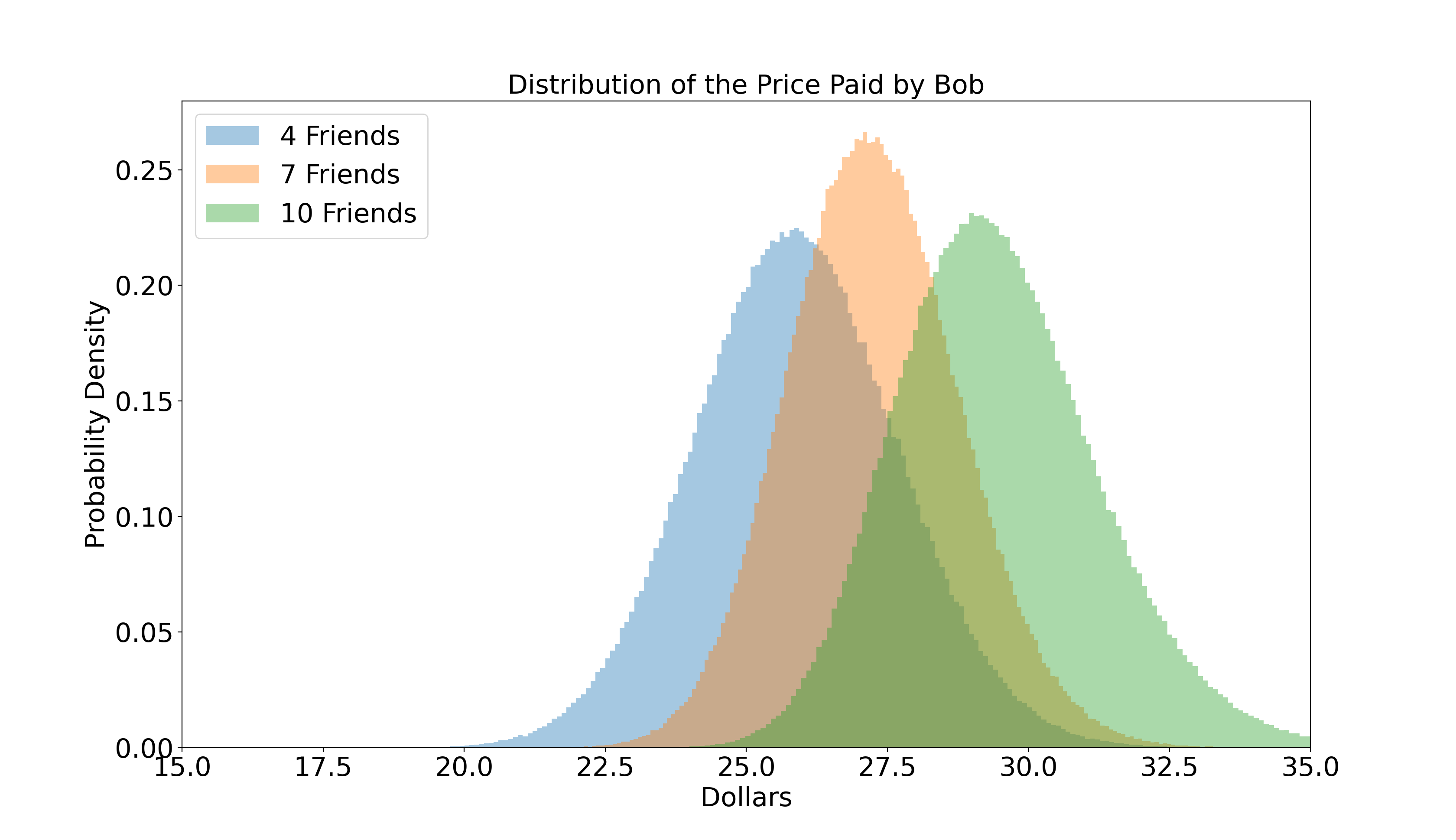
In this simulation, Bob usually paid more for the jar of coins than it is worth. This happened almost every time with just ten of Alice’s friends participating in the auction. Also notice, the more participants the auction has, the worse the winner’s curse becomes.
This shows that when you’ve estimated the value of an item in an auction, you should reduce your bid, not just to account for auction dynamics, but also to account for uncertainty in your valuation. In particular, despite conventional wisdom saying to bid your true valuation in a second-price auction, you should actually reduce your bid a bit in most real-world situations.
Observing of the Curse
Now that we understand the winner’s curse, we can see what it looks like in some real data. There are two places we observe the winner’s curse at NextRoll. When an ad exchange notifies us of an ad opportunity, we have to select an ad for which to bid. This is done via an internal auction and is the first place this effect manifests. Next, we submit the highest internal bid to the ad exchange, and an auction is run amongst bidders like NextRoll. This external auction is the second place we observe the winner’s curse.
To be clear, I highlight these instances of the winner’s curse because the effect is interesting, not because these cases are particularly problematic. Unlike in the example of Bob losing money by purchasing Alice’s jar of coins, the impact of the winner’s curse on NextRoll’s bidding systems is minor overall.
The Internal Auction
The internal auction is where we decide which ad from our thousands of advertisers will be submitted to the external auction. Some of this decision is made for us by simply applying the advertiser’s targeting criteria. Selecting among the remaining advertisers’ eligible ads is done with an auction that has two steps.
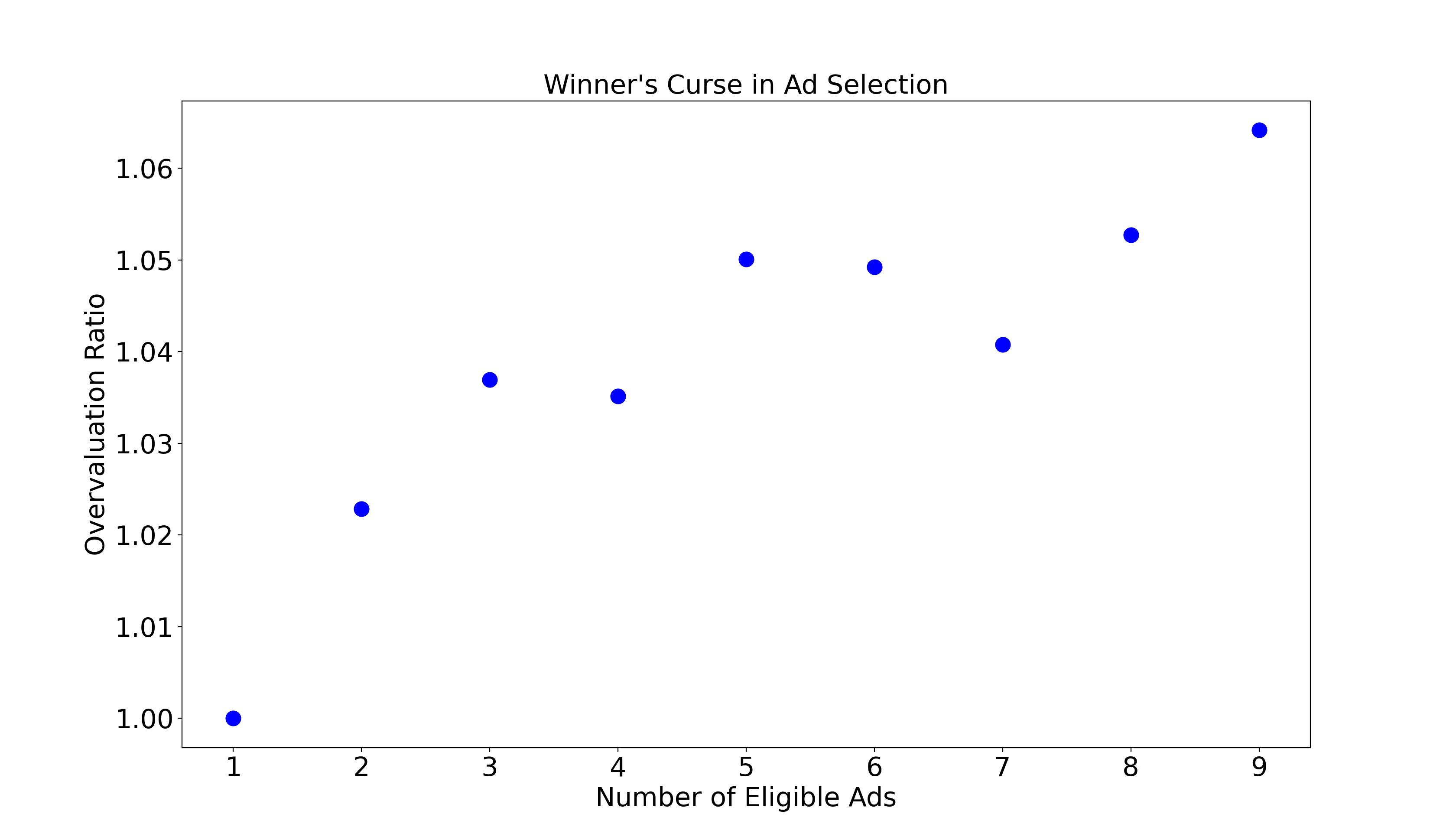
First, we select the most valuable eligible ad for each advertiser. As you can see below, the more ads from which we have to select for a given advertiser, the more overvalued the selected ad is. This is analogous to the winner of Alice’s auction paying more for the jar of coins when there are more bidders. This is the winner’s curse in action!
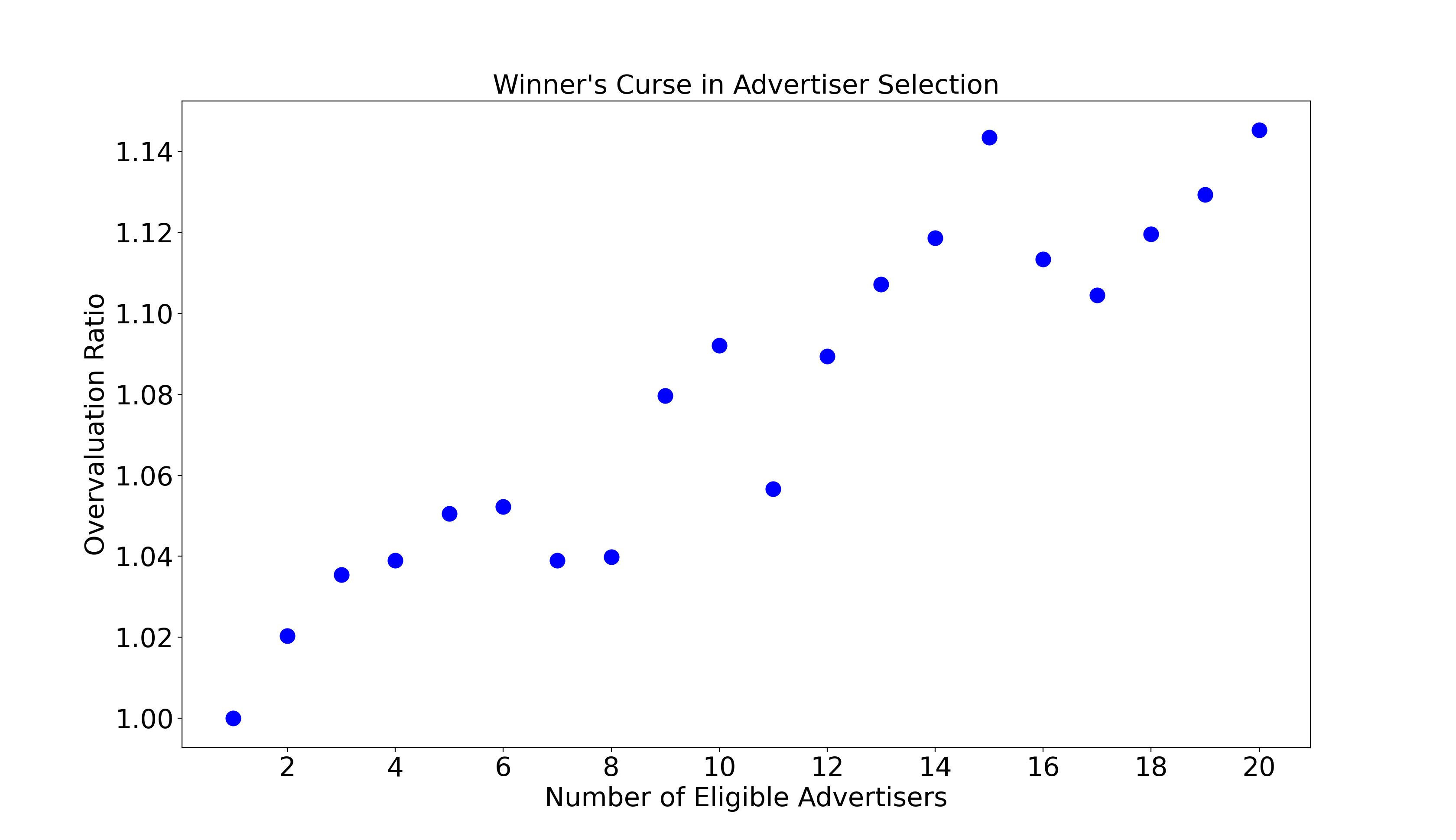
The second step in the internal auction is to choose the most valuable ad amongst each advertisers’ best candidates. As in the case above, the more advertisers targeting the opportunity, the more overvalued the selected ad is. Again, this is the winner’s curse.
The External Auction
Once we have decided which ad to select and what to bid for it, we send that information to the ad exchange. The exchange runs another auction, and based on the results, makes the final decision on which ad to show. Unlike in our internal auction, we are not the auctioneer in the external auction, which means we don’t have complete information about the auction’s bids. This makes confidently observing the winner’s curse more challenging.
The first sign of the winner’s curse in the external auction is that we consistently predict ad impressions to be slightly more valuable than they turn out to be. To have confidence that these overvaluations really are the winner’s curse, rather than an undiscovered bug, we will need to understand a bit about the interaction between our machine learning and the external auction.
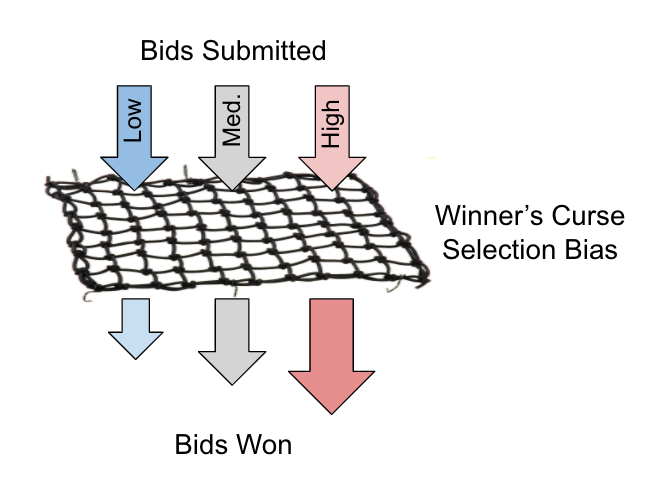
The key thing to understand is that the valuations predicted by our machine learning system are very closely related to when we win the external auction. In particular, when our models overvalue a potential impression, we tend to bid higher, which causes us to win the auction more often. In other words, we win a disproportionate amount of the bids whose value we overestimate. This selection bias is visualized below.
Fortunately, when we win the external auction and show an ad, we receive feedback on the ad’s correct value. This, in turn, feeds into our machine learning models as training data. As a result, mistakes made by previous iterations of the model are corrected. Unfortunately, no model is perfect, and our newer model iteration will make new mistakes.
The crucial insight for our investigation is that by comparing the predictions (and mistakes) made by older and newer model iterations over the same slice of backtesting data, we can learn whether the overvaluations we observe are, in fact, caused by the winner’s curse, or more menacingly, an undiscovered bug.
To make this concrete, let’s say that we trained model A ten days ago, and that we trained model B yesterday. Consider what we would expect to happen if we used both models A and B to predict over yesterday’s ad impression data that model B bid on and purchased. If the winner’s curse were the cause of the overvaluations in the external auction, we’d expect model B to overvalue these impressions that it purchased because of the selection bias discussed above. We’d also expect model A to value these impressions accurately. This is because this selection bias affecting model B does not apply to model A, since it was not used to bid on and purchase these impressions.
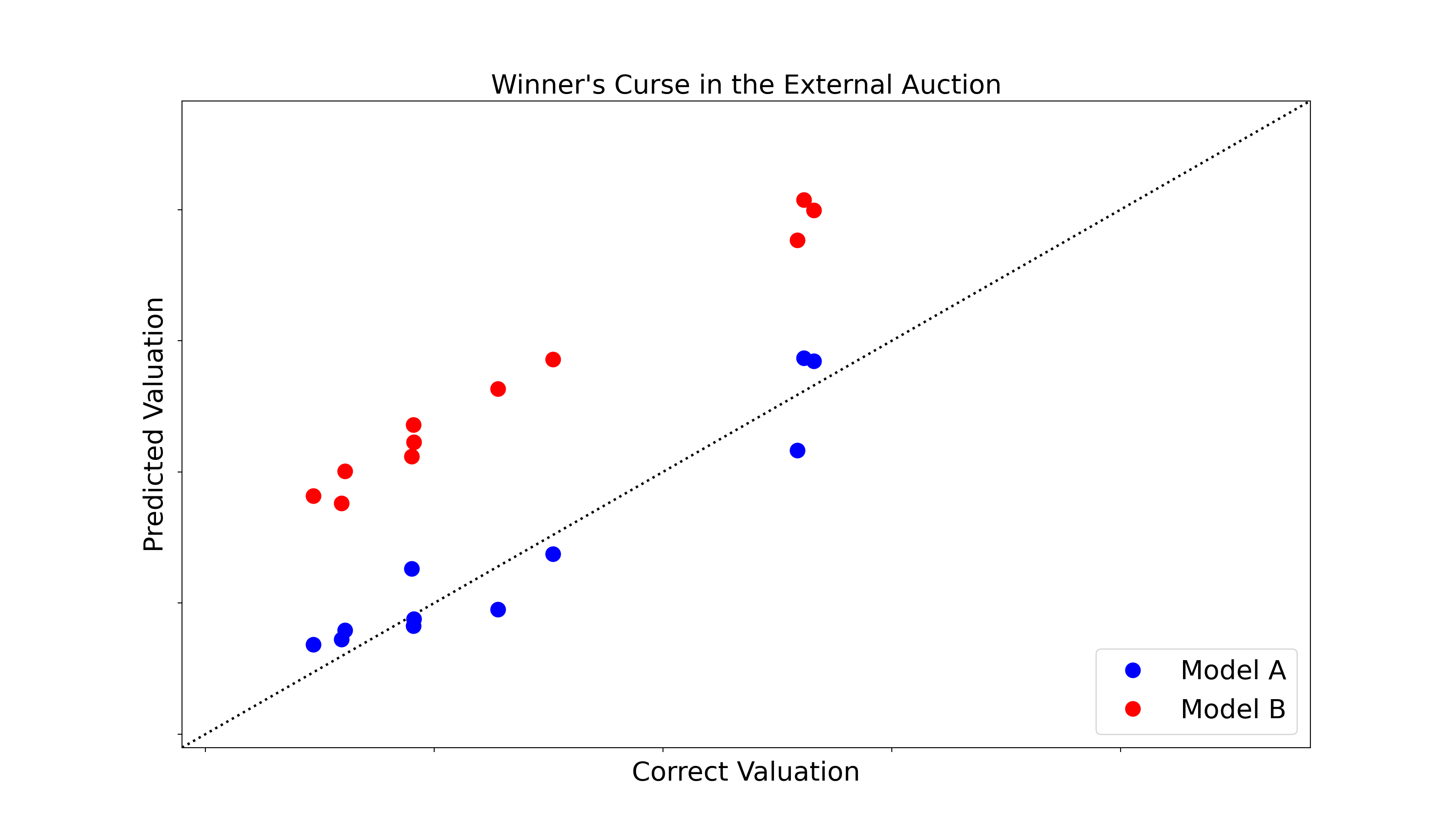
The plot above shows this experiment run over real data on 11 different days. As you can see, model A does not overvalue the ad impressions purchased by model B. This means we really are observing the winner’s curse in the external auction!
Conclusion
You’re more likely to win an auction when you bid too high. That is the essence of the winner’s curse, a surprisingly simple, yet counter-intuitive, statistical effect. In this post, we learned how the curse works in theory, and we observed it in some real data.
Often, those of us interested in auctions ignore the fact that bidders estimate the value of an item, assuming instead that they know it exactly. However, bidders having uncertain valuations is all that’s needed for the winner’s curse to appear. When the curse strikes, buyers realize less profit than expected from the auctions in which they participate. In extreme cases, this effect can even result in the buyer losing money, as we saw with Bob and Alice. Beware of the curse!