Questioning Second-Price Auctions in Ad Tech

Written by Matthew B. Wilson, December 21, 2018

Introduction

A primary responsibility of the data science team at the AdRoll Group is to determine what we should bid in real-time auctions for ad inventory. Among other things, our bid price is dependent on the type of auction in which we are participating.

Second-price auctions, where the highest bidder wins and pays the second highest bid price, are popular in ad tech because they incentivize bidders, such as AdRoll, to bid their true value for the ad impression being auctioned ⁽¹⁾. First-price auctions, where the highest bidder wins and pays their bid, are also popular, but they incentivize bidders to reduce their bids below their valuation. Exchanges communicate the auction type to bidders, like us, in the bid request. From the perspective of ad exchanges, there exists a (shortsighted) incentive to make bidders believe they are bidding into second price auctions, so they bid their true valuation, while charging them something more than the second price.

In this post, we consider only auctions in which we are explicitly told the auction is second-price. We will examine how our clearing prices compare to our bid prices in these second-price auctions, and we will observe some irregular patterns that lead us to question whether these auctions really are second-price. We will then discuss the algorithmic defense against misspecified auction mechanisms that we’ve developed at the AdRoll Group.

Questioning Auction Mechanisms

In this section we will examine how our clearing prices compare to our bid prices in what are supposed to be second-price auctions on four exchanges, each displaying a unique relationship between clearing prices and bid prices. We will do this in two ways, and in both cases we will observe some questionable patterns. First, we will graphically examine how clearing prices are related to the bid prices in second-price auctions. Second, we will compare the empirical utility we gain from second-price auctions to theoretical calculations.

Graphical Analysis of Second-Price Auctions

In this subsection we will look at histograms of the ratios of our clearing price to our bid price, and scatter plots of our clearing prices as a function of our bid prices.

Exchange A

We begin with an exchange that we believe runs true second-price auctions, for the most part. One reason we believe this is that we regularly win impressions for a small fraction of our bid price, as you can see in the plots below. The only odd feature in these plots is that we sometimes pay what we bid, but compared to other exchanges this effect is very mild.

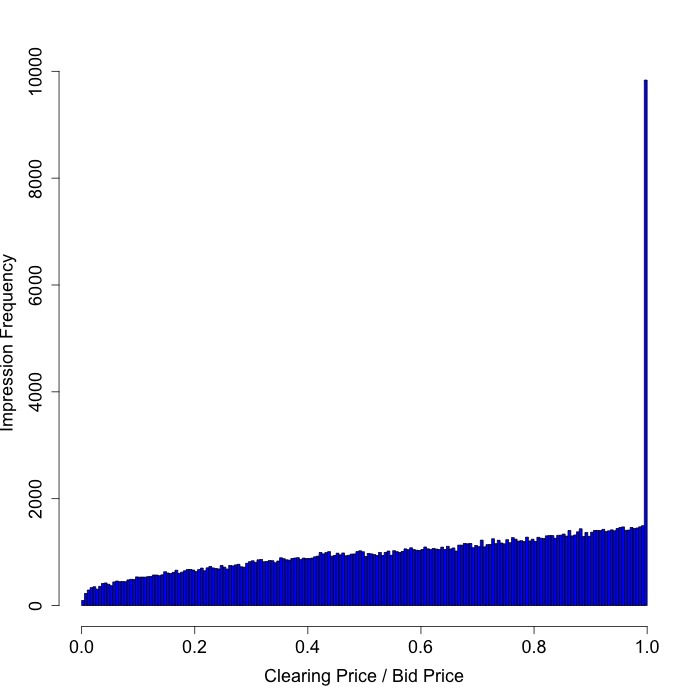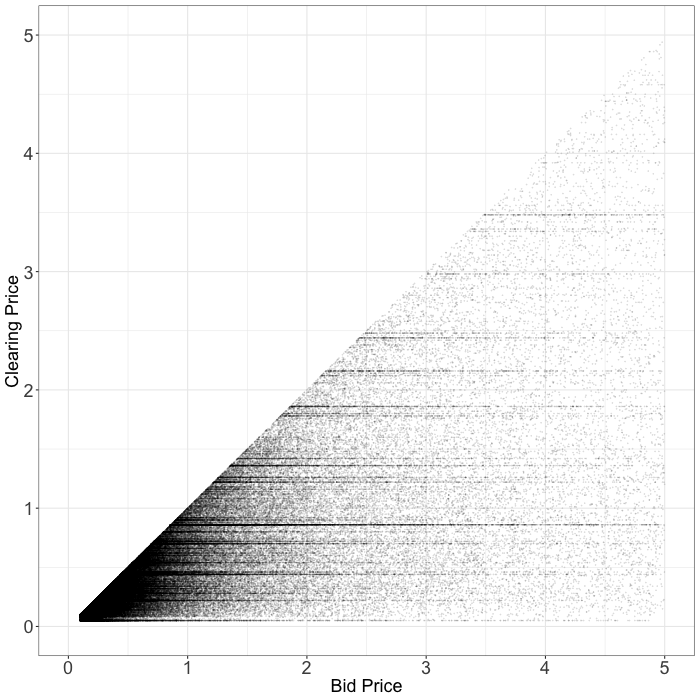Exchange B

Next, we analyze an exchange whose second-price auctions we have reason to question. On this exchange we almost never win impressions for a small fraction of our bid price. Most of the time we end up paying exactly what we bid. In fact, these auctions look more like first-price auctions than second-price auctions.

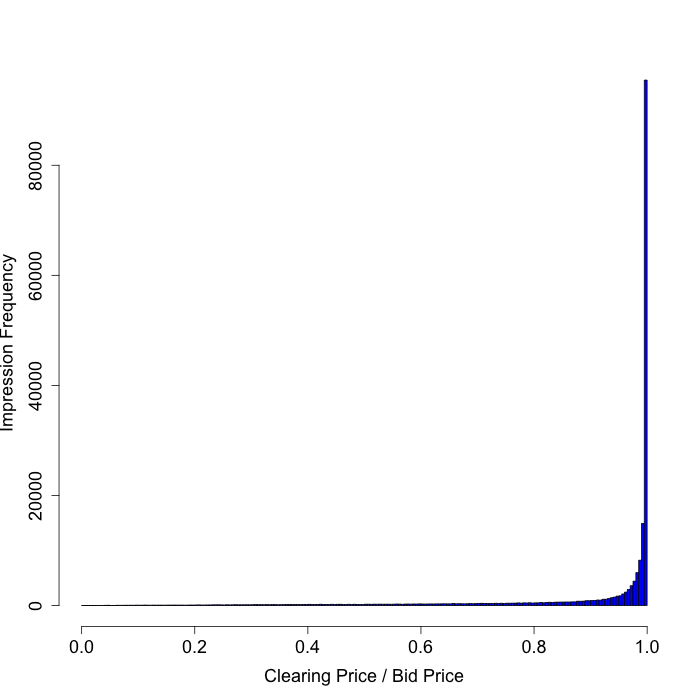Exchange C

Here is another exchange whose second-price auctions are irregular ⁽²⁾. On this exchange, as with the previous exchange, we see that we are often charged exactly what we bid. Moreover, we are often charged roughly 90% of our bid price. How can the second-price in an auction so frequently be a function of our bid price?

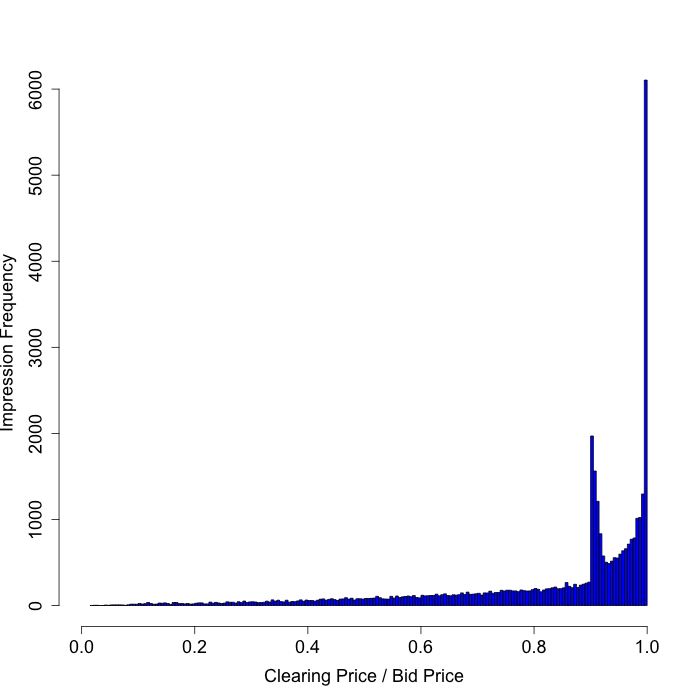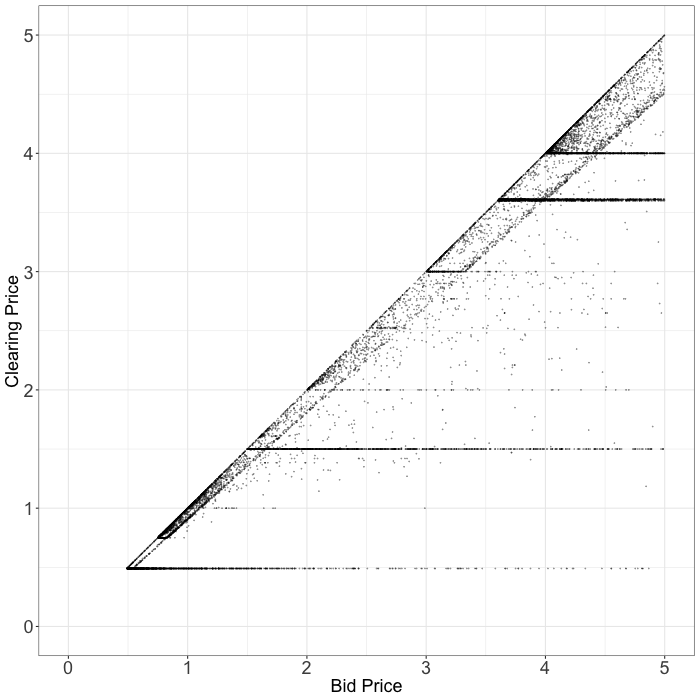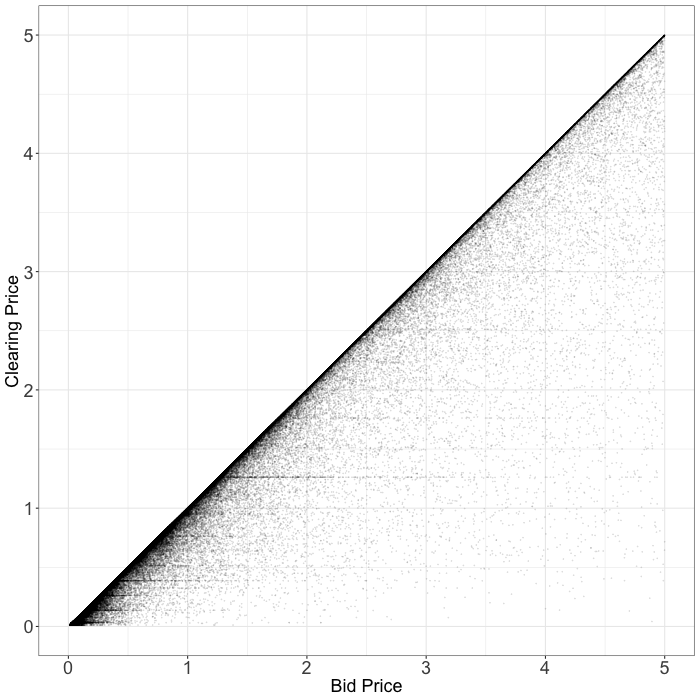
Exchange D

This exchange does not exhibit the same strange patterns as “Exchange B” or “Exchange C”. Nonetheless, we almost never win impressions for a small fraction of our bid price. Put another way, the bottom right corner of the scatter plot below is conspicuously empty. Can this really arise from second price auctions?

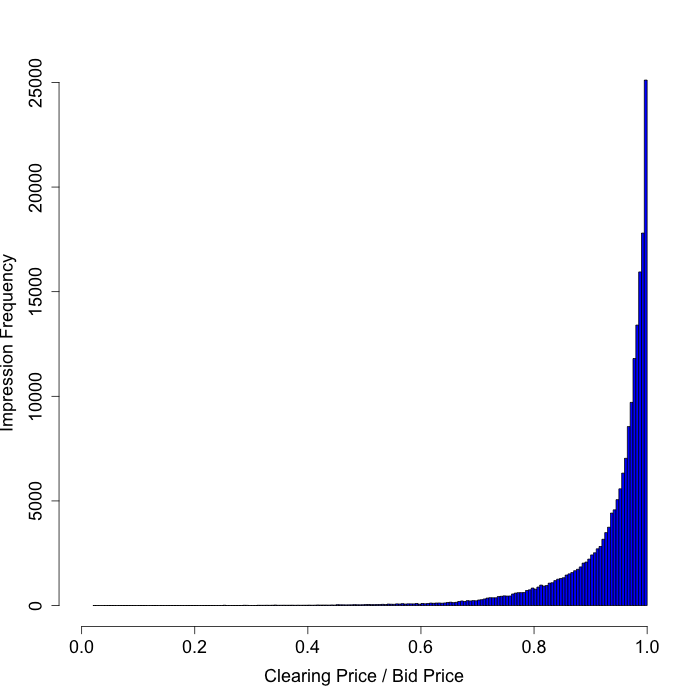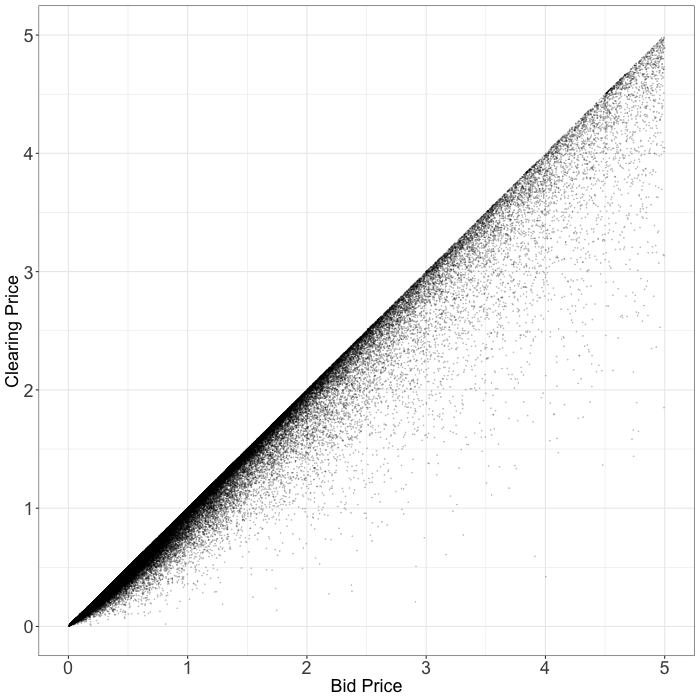Analysis of Utility in Second-Price Auctions

In this subsection we will analyze second-price auctions by comparing the utility we realize empirically to the utility we theoretically expect to realize. Assume we are in a second-price auction, and let \(M\) be a random variable representing the highest bid among all other auction participants with PDF \(f_M\) and CDF \(F_M\). The fact that we are in a second-price auction implies our bid \(b\) should be our valuation \(v\). We will win the auction when \(M < v\), and the utility we realize when we win is \(v-M\). Putting this together, the expected utility in second-price auctions \(U_{SP}\) can be written as

$$U_{SP} = E\left[\mathbb{1}_{\{M<v\}}\left(v-M\right)\right]$$

Chris Evans, a Staff Data Science Engineer at the AdRoll Group, worked out a very nice result for this quantity. Following the derivation of the tail-sum formula for expectation, we have ⁽³⁾:

$$\begin{align*} U_{SP} &= \int_0^v (v-m) \ f_M(m) \ dm && \text{Definition of expectation.} \\ &= \int_0^v \left( \int_0^\infty \mathbb{1}_{\{(v-m)>x\}}\ dx \right) f_M(m) \ dm && \text{Rewrite with indicator.}\\ &= \int_0^\infty \left( \int_0^v \mathbb{1}_{\{(v-m)>x\}}\ f_M(m) \ dm \right) dx && \text{Exchange order of integration.}\\ &= \int_0^\infty F_M(v-x)\ dx && \text{Definition of CDF.}\\ &= \int_0^v F_M(x)\ dx && \text{Change of variables.} \end{align*}$$

This result enables us to predict the utility we will realize in a second-price auction given \(F_M(x)\), information about how the bids of other bidders are distributed. Fortunately, we had already developed an accurate model to predict \(F_M(x)\) for other applications, as we will see in the next section. Now that we are able to calculate the predicted utility we can compare it to the empirically realized utility. Below we can see a plot of the average utility empirically realized for different (binned) values of predicted utility.

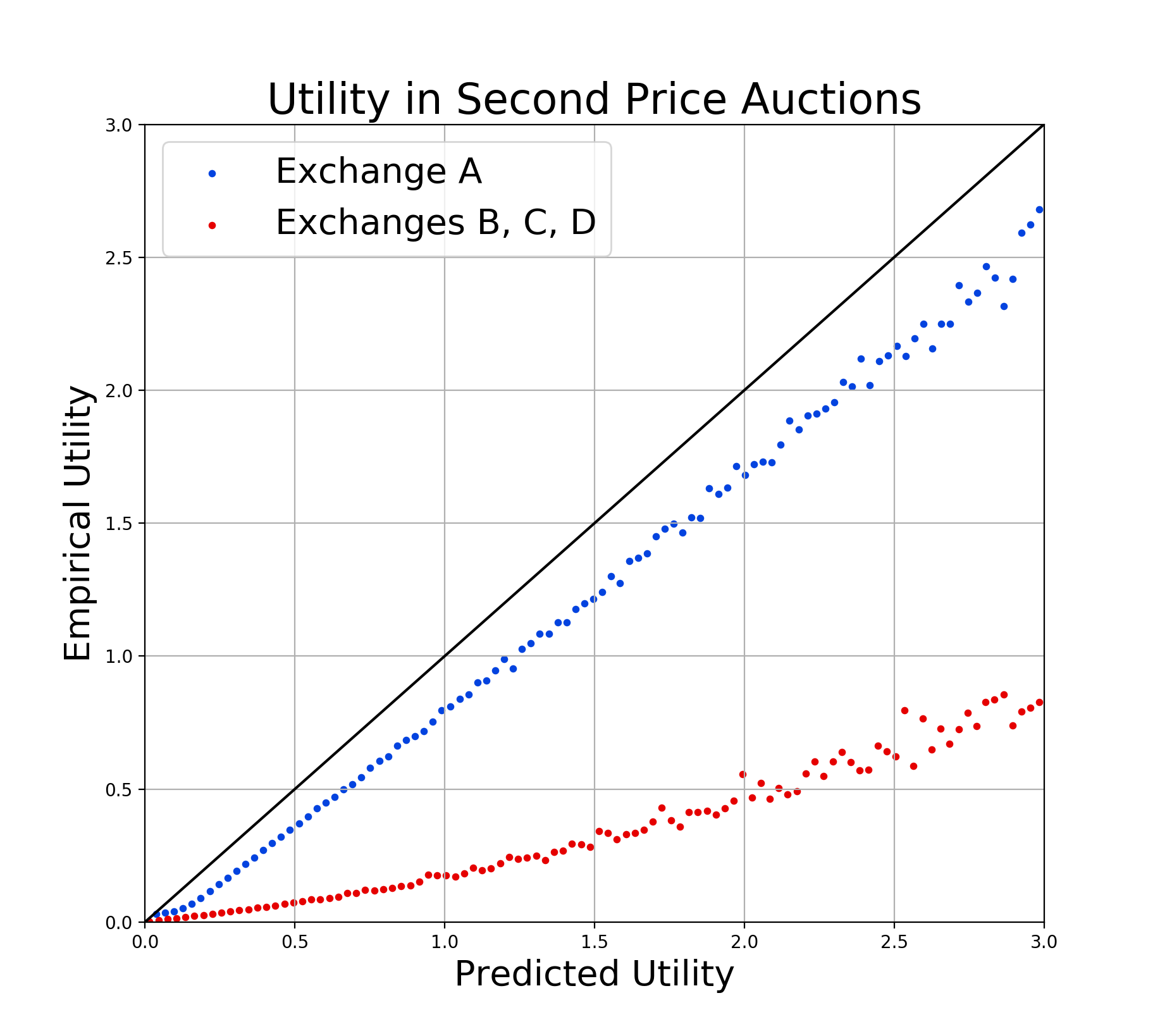
As this figure shows, this calculation predicts we will realize much more utility than we do for the three exchanges where we saw irregular auction mechanisms (namely, B, C, and D). On the other hand, this calculation comes fairly close to correctly predicting the utility we will realize in the case of “Exchange A”, where the auction mechanisms look truly second-price. This plot is another reason to question the auction mechanisms as communicated by some exchanges, and further highlights our need for an algorithmic response.

Responding to Auction Mechanisms

In this section we will discuss the algorithmic defenses we have built in response to misspecified auction mechanisms. As background, we will first discuss bidding into auctions with well-specified auction mechanisms.

Bidding into Specified Auction Mechanisms

Ideally, we would know the exact auction mechanism into which we are bidding because it affects our optimal bid. With knowledge of the true auction mechanism, we’d have an understanding of how the cost \(C\) of the impression varies as a function of our bid. For example, in a first-price auction, where we pay what we bid, \(C(b) = b\). Given \(C\) we can compute the expected utility for our bid as

$$U(b) = E\left[ \mathbb{1}_{\{M<b\}}\left(v - C(b) \right)\right] \\ $$

Ryoma Canastra, a Data Science Engineer at the AdRoll Group, proved that to maximize the value we provide to customers, each bid we submit should be chosen to maximize \(U\) ⁽⁴⁾. For example, in a first-price auction our bid \(b_{FP}\) for an impression we valued at \(v\) dollars would be ⁽⁵⁾

$$\begin{align*} b_{FP} &= \text{argmax}_{b} \ E\left[ \mathbb{1}_{\{M<b\}}\left(v - b \right)\right] \\ &= \text{argmax}_{b} \ F_M(b) \left(v - b \right) \end{align*}$$

Bidding into Misspecified Auction Mechanisms

Without knowledge of the auction mechanism we cannot bid in the theoretically optimal way. Instead, we have to resort to a more empirical approach. The approach we’ve settled on is quite simple. When we aren’t confident in the auction mechanism, we predict it.

Specifically, we predict \(p_{FP}\), the probability the auction will result in us paying something close to first-price. To simplify things, we assume there are only first and second price auctions, and train a classifier to differentiate these cases. The more confident we are in having to pay a large fraction of our bid price, the more we reduce our bid. In particular, we bid

$$\begin{align*} b &= p_{FP} \ b_{FP} + (1 - p_{FP}) \ v \end{align*}$$

This approach has a few nice properties. First, this approach reduces to optimal behavior when we are confident in the auction mechanism. For example, when we are confident that we are in a first price auction (\(p_{FP} = 1\)) we will bid \(b_{FP}\), which is optimal. Similarly, when we are confident that we are in a second-price auction (\(p_{FP} = 0\)) we will bid \(v\), which is also optimal. Second, this approach learns and updates our bids as auction mechanisms change. Third, this approach is scalable, requiring minimal human intervention. Most important, we like this approach because it has performed well in A/B tests, capturing significantly more utility for us on behalf of our customers than submitting the optimal bid for the auction type passed by exchanges.

Conclusion

In the first section of this post we saw evidence that second-price auctions in ad tech may not always be purely second-price. First, we saw irregularities in plots relating our clearing prices to our bid prices in what were supposed to be second-price auctions. Next, we saw that the utility we realize in the questionable second-price auctions is much less than theory would predict.

That said, in some cases there may be harmless explanations for the observations of this blog post. It’s possible that header bidding or different bid densities in the different exchanges could cause qualitatively different clearing price vs. bid price behavior. Or, perhaps we are miscommunicating with certain exchanges about the type of auctions in which we are participating.

Nonetheless, we have decided to defend against the possibility of misspecified auction mechanisms. In the second section of this post we saw an approach for algorithmically defending against opaque auction mechanisms, one of the many ways the data science team is working to deliver maximal value for our customers.

Footnotes

1. The Vickrey auction Wikipedia page explains why bidding your valuation is optimal in a second-price auction.
2. We only consider a subset of second-price auctions for this exchange. These are all private marketplace deals understood to be second-price auctions.
3. Section 1.2.1 of these course notes has a proof of the discrete tail-sum formula.
4. The details are beyond the scope of this post.
5. This was the original reason we developed \(F_M(x)\), which we used in the first section to predict the utility realized in a second-price auction.

---