Thompson Sampling and Bayesian Factorization Machines

Written by Constantin Berzan, March 06, 2017

On the Data Science Engineering team, we are constantly working to improve the machine learning systems powering AdRoll’s products. We have recently started investigating Thompson sampling and Bayesian Factorization Machines as a way to ensure efficient exploration of the ad marketplace. In this post, I will illustrate why such exploration is necessary, and then dive into some of the math and algorithms required to make it work. Credit for inspiring this project goes to the paper “An Empirical Evaluation of Thompson Sampling,” by Olivier Chapelle and Lihong Li. We worked through a derivation of their approach, and then extended it to work with our Factorization Machines model.

Motivation

One of the central problems we solve at AdRoll is deciding which ad to show to a given user browsing a given page on the Web. We have to make these decisions in an environment that is constantly changing, as new ads get added to our system, old ads get retired, and users appear, disappear, or change their browsing behaviors. In mathematical terms, we say that the distribution we are trying to model is non-stationary.

This non-stationary regime means that there is always some uncertainty about which decision is optimal, and each sequential decision gives us additional information that we can use to make better decisions in the future. In other words, we have a classical exploration vs. exploitation tradeoff from reinforcement learning.

To illustrate this, consider a simple example where we have two ads to choose from: Ad 1 has a predicted conversion probability of 0.123, and we have shown this ad many times before, so we are fairly certain in our estimate. Ad 2 has a predicted conversion probability of 0.111, but we’ve only shown it a few times, so its true value could be a bit higher or a bit lower. We have two options:

Exploit what we already know, and choose Ad 1 because it has a higher predicted conversion probability.
Explore and choose Ad 2, in order to get more knowledge about it and improve our decisions in the future.

After sufficient exploration, the conversion probability of Ad 2 could turn out to be 0.100, in which case Ad 1 is much better and the exploration did not pay off. On the other hand, Ad 2’s probability could turn out to be 0.130, in which case it is better than Ad 1, and we wouldn’t have discovered this without taking a chance on Ad 2. Exploration allows us to make better-informed decisions going forward, but there is no way to tell ahead of time whether we will find a better ad this way.

It is clear that some amount of exploration is necessary, otherwise our system would always show old ads known to perform well, and never show any new ads that our customers upload. On the other hand, it is also clear that excessive exploration is wasteful: once we have done enough exploration to determine that Ad 1 is much better than Ad 2, there is no need to continue showing Ad 2 anymore.

One naïve explore/exploit strategy is to always explore on X% of traffic, by showing a random ad, and always exploit on the remaining (100 - X)% of traffic, by showing the best-known ad. This epsilon-greedy strategy is simple to implement, but it is hard to tell if it performs too much or too little exploration. Ideally, we would like a system that adjusts the amount of exploration dynamically, based on how uncertain it is about the value of each decision.

Now that we understand the problem intuitively, it’s time to formalize it and describe our solution.

Contextual Bandits

Our problem can be formulated as a contextual multi-armed bandit, where we are playing a sequential decision game. At each iteration, we get a context vector $x$, which is a feature vector containing all the relevant information about the user and the page they are visiting. We choose an action $a$ from a set of available actions $A$, which in our case is the set of ads to show. Some time later, we receive a reward $r$, which is 1 if the user converted, and 0 otherwise. Our goal is to choose actions in a way that maximizes cumulative reward.

One obvious way to approach action selection is to build a predictive model of the reward given a context and an action: $P(r|x,a)$. We can use our existing Factorization Machines (FM) model to do this, by just merging the context features $x$ and the ad features $a$ into a single feature vector. At each iteration, we would “score” each action $a$ by computing $P(r|x,a)$ using our model, and then we’d have to decide whether to explore or exploit.

Thompson Sampling

It turns out that by taking a Bayesian approach, we can solve our explore/exploit dilemma in a very elegant way. Consider our model from before, $P(r|x,a)$. This model is parameterized by some set of parameters $\theta$, for example, the set of weights in logistic regression or FM. In a non-Bayesian setting, we have some optimization algorithm that finds a maximum-likelihood estimate for $\theta$, which is equivalent to minimizing logistic loss on the training set. In a Bayesian setting, we place a prior $P(\theta)$ on the parameters, and use Bayes’ Rule to express the posterior after observing some training data:

$P(\theta|x_{1:N},a_{1:N},r_{1:N}) \propto P(\theta) \prod_{i=1}^N P(r_i|x_i,a_i,\theta)$

We could use this to obtain a maximum a posteriori estimate of $P(r|x,a)$ by integrating over the unobserved $\theta$, but that is not our goal. Instead, we will use the simple but powerful idea of Thompson sampling to solve our explore/exploit dilemma. This consists of two steps:

Sample a set of parameters according to the posterior after seeing the training data: $\theta' \sim P(\theta|x_{1:N},a_{1:N},r_{1:N})$.
Choose the action that is optimal with respect to the sampled set of parameters: $\hat{a} = \mathop{\arg\max}_a P(r|x,a,\theta')$.

For an intuitive understanding of Thompson sampling, consider what would happen if we had very little training data. The posterior over parameters would be broad, and the $\theta'$ samples in each iteration would have high variance. Thus, there would be a lot of randomness in the chosen actions $\hat{a}$, which is exactly the definition of exploration. As we collect more training data, the posterior over parameters becomes more peaked, and both the samples of $\theta'$ and the chosen actions $\hat{a}$ become more stable, which is exactly the definition of exploitation. To summarize, the system starts out with a lot of exploration, and automatically adjusts towards more exploitation as it become more certain in its belief about the parameters.

Notice that in our introductory example, we talked about exploration at the ad level: Ad 1 had a high conversion rate with high certainty, while Ad 2 had a lower conversion rate but with a lot of uncertainty. Thompson sampling is a little more subtle, because it performs exploration at the parameter level; it will automatically explore to decrease uncertainty about the parameters in the model. This is an advantage in our application, since we use the hashing trick to keep our parameter space fixed, while ads appear and disappear all the time.

Now that we understand how Thompson sampling works, let’s see how to represent and update the posterior over parameters in the case of logistic regression and factorization machines.

Common Notation

We have a training set of $N$ examples $(\mathbf{x}_i, y_i)$, where the feature vector is a $D$-dimensional vector: $\mathbf{x}_i \in \mathbb{R}^D$ and the label is binary: $y_i \in \{0, 1\}$. We will use $i$ to index examples whenever possible.

For a linear model (traditional logistic regression), the parameters $\theta$ are just a weight vector $\mathbf{w} \in \mathbb{R}^D$. We will use $j$ to index into the weight vector whenever possible.

For a factorization machines (FM) model, the parameters $\theta$ are a vector $\mathbf{w} \in \mathbb{R}^D$ as above, and also a matrix $\mathbf{V} \in \mathbb{R}^{D \times K}$, where $K$ is the number of factors. We will use $j$ to index into $\mathbf{w}$ and $jk$ to index into $\mathbf{V}$ whenever possible (we omit the comma when we have multiple indices).

We define $\mu_i$ to be the probability of a positive label for example $i$:

$\mu_i ~=~ p(y_i=1 | \mathbf{x}_i) ~=~ \frac{1}{1 + \exp(-F(\mathbf{x}_i))}$

where $F$ is a kernel, or model equation. For the linear case, $F$ is just a dot product of the weights with the features, and for factorization machines, $F$ captures second-order interactions:

$\begin{align} F_\text{linear}(\mathbf{x}_i) &= \sum_{j=1}^D{ w_j x_{ij} } \\ F_\text{FM}(\mathbf{x}_i) &= \sum_{j=1}^D{ w_j x_{ij} } + \sum_{a=1}^D{ \sum_{b=a+1}^D{ \langle \mathbf{V}_a, \mathbf{V}_b \rangle x_{ia} x_{ib} } } \end{align}$

(For simplicity, we omit the bias term in each model.)

In both cases, the log-likelihood of the training set is given by:

$\text{loglik}(\theta) = \sum_{i=1}^N{( y_i \ln \mu_i + (1-y_i) \ln (1-\mu_i) )}$

where the $\mu_i$ terms use either $F_\text{linear}$ or $F_\text{FM}$ depending on the model.

The Laplace Approximation

For a Bayesian treatment of logistic regression, we want to put a prior on the parameters $\theta$ and compute the posterior given observed data. We choose a simple prior where the parameters are independent, and each parameter is drawn from a normal distribution with its own mean $m$ and precision $s$:

$\begin{align} w_j &\sim \mathcal{N}(m_j, s_j^{-1}) \\ v_{jk} &\sim \mathcal{N}(m_{jk}, s_{jk}^{-1}) \end{align}$

Using Bayes’ Rule, the posterior is proportional to the prior and likelihood:

$p(\mathbf{w} | \mathbf{x}_{1..N}, y_{1..N}) ~\propto~ p(\mathbf{w}) \cdot p(y_{1..N} | \mathbf{w}, \mathbf{x}_{1..N})$

Unfortunately, this posterior is not a normal distribution. But we can approximate it with a normal distribution by using the Laplace approximation (see section 4.4 in Bishop’s “Pattern Recognition and Machine Learning” textbook). That way, the approximated posterior will have the same form as the prior, allowing us to iteratively update our belief about the parameters.

The Laplace approximation is a technique for approximating an arbitrary distribution $p(z) = c^{-1} f(z)$ (where $f$ is an arbitrary function and $c$ is a normalization term) with a normal distribution $q(z) = \mathcal{N}(z_0, A^{-1})$ where $z_0$ is a mode of $f(z)$, and $A$ is the negative second derivative of $\ln f(z)$, evaluated at $z_0$:

$\begin{align} \frac{\mathrm{d} f(z)}{\mathrm{d} z} &\Bigr|_{z=z_0} = 0 \\ A = \frac{-\mathrm{d}^2 \ln f(z)}{\mathrm{d} z^2} &\Bigr|_{z=z_0} \end{align}$

The first step is to find a mode of the posterior distribution. We can do this by finding a maximum a posteriori (MAP) estimate of the parameters. This is equivalent to maximizing the log-posterior:

$\text{logpost}(\theta) = \ln p(\theta) + \text{loglik}(\theta)$

The second step is to find the $A$ term, which is the negative second derivative of $\text{logpost}(\theta)$ with respect to each parameter. (We keep things simple by forcing our parameters to be independent.)

Before making these calculations concrete for the linear and FM kernels, we show a general result that will greatly simplify those calculations. Consider the partial derivative of $\text{loglik}(\theta)$ with respect to some variable $z$:

$\frac{\partial}{\partial z} \text{loglik}(\theta) ~=~ \sum_{i=1}^N{ \left( \frac{y_i}{\mu_i} - \frac{1-y_i}{1-\mu_i} \right) \frac{\partial \mu_i}{\partial F(\mathbf{x}_i)} \frac{\partial F(\mathbf{x}_i)}{\partial z} }$

Note that $\mu_i$ is a logistic function of $F(\mathbf{x}_i)$, with the useful property that $\partial \mu_i / \partial F(\mathbf{x}_i) = \mu_i (1 - \mu_i)$. Therefore our derivative simplifies to:

$\frac{\partial}{\partial z} \text{loglik}(\theta) ~=~ \sum_{i=1}^N{ (y_i - \mu_i) \frac{\partial F(\mathbf{x}_i)}{\partial z} }$

We now take the second derivative:

$\frac{\partial^2}{\partial z^2} \text{loglik}(\theta) ~=~ \sum_{i=1}^N{\left( - \mu_i (1 - \mu_i) \left(\frac{\partial F(\mathbf{x}_i)}{\partial z}\right)^2 + (y_i - \mu_i) \frac{\partial^2 F(\mathbf{x}_i)}{\partial z^2} \right)}$

To make this concrete for the linear and FM kernels, we only need to evaluate the terms $\frac{\partial F(\mathbf{x}_i)}{\partial z}$ and $\frac{\partial^2 F(\mathbf{x}_i)}{\partial z^2}$ for the relevant model equation $F$ and parameter $z$, and plug them into the equation above.

Bayesian Logistic Regression

For logistic regression with the traditional linear kernel, the log-posterior is:

$\begin{align} \text{logpost}(\mathbf{w}) &~=~ \ln p(\mathbf{w}) + \text{loglik}(\mathbf{w}) \nonumber \\ &~=~ \text{const} - \frac{1}{2} \sum_{j=1}^D{ s_j (w_j - m_j)^2 } + \sum_{i=1}^N{( y_i \ln \mu_i + (1-y_i) \ln (1-\mu_i) )} \tag{1} \end{align}$

With a bit of work, the second derivative of the log-posterior turns out to be:

$\begin{align} \label{a-lr} A_j = - \frac{\partial^2}{\partial w_j^2} \text{logpost}(\mathbf{w}) &~=~ - \frac{\partial^2}{\partial w_j^2} \ln p(\mathbf{w}) - \frac{\partial^2}{\partial w_j^2} \text{loglik}(\mathbf{w}) \nonumber \\ &~=~ s_j + \sum_{i=1}^N{ \mu_i (1 - \mu_i) x_{ij}^2 } \tag{2} \end{align}$

We now have everything we need to express the Bayesian Logistic Regression algorithm. It maintains the following invariant: after processing $t$ batches, the weights are distributed as $w_j \sim \mathcal{N}(m_j^{(t)}, 1/s_j^{(t)})$, which is an approximation of the true posterior after all the data observed so far. In the algorithm below, we update the means $m_j$ and precisions $s_j$ in place, so we omit the superscripts $(t)$.

Algorithm: Bayesian Logistic Regression

Initialize the prior on each weight $w_j$ with $m_j = 0$, $s_j = \lambda$.
For each new batch of training data $(\mathbf{x}_i, y_i)$ for $i = 1 .. N$:
- Find $\hat{\mathbf{w}}$ maximizing equation (1) by numerical optimization.
- Compute $A_j$ for each weight according to equation (2).
- Update the weight distribution: $m_j \gets \hat{w}_j$ and $s_j \gets A_j$.

Our priors have a natural interpretation. By starting with the prior $w_j \sim \mathcal{N}(0, \lambda^{-1})$, our objective function in equation (1) is exactly the same as for (non-Bayesian) Logistic Regression with an L2 regularizer $\lambda$.

The algorithm above matches algorithm 3 derived by Chapelle and Li, confirming that we have derived the Laplace approximation correctly. The only difference is one of notation: our labels are in $\{0, 1\}$ while their labels are in $\{-1, 1\}$, so their objective function has a slightly different form.

Bayesian Factorization Machines

For logistic regression with the FM kernel, the log-posterior is:

$\begin{align} \text{logpost}(\mathbf{w}, \mathbf{V}) &~=~ \ln p(\mathbf{w}, \mathbf{V}) + \text{loglik}(\mathbf{w}, \mathbf{V}) \nonumber \\ &~=~ \text{const} - \frac{1}{2} \sum_{j=1}^D{ s_j (w_j - m_j)^2 } - \frac{1}{2} \sum_{j=1}^D \sum_{k=1}^K{ s_{jk} (v_{jk} - m_{jk})^2 } \nonumber \\ &\phantom{~=~ const} + \sum_{i=1}^N{( y_i \ln \mu_i + (1-y_i) \ln (1-\mu_i) )} \tag{3} \end{align}$

Since our parameters are the weights $w_j$ and the $\mathbf{V}$ matrix entries $v_{jk}$, we need second derivatives with respect to both of these in order to use the Laplace approximation.

The second derivative of the log-posterior w.r.t. $w_j$ has the same form as for the linear kernel, except that the $\mu_i$ terms now use the FM kernel:

$\begin{align} A_j = - \frac{\partial^2}{\partial w_j^2} \text{logpost}(\mathbf{w}, \mathbf{V}) &~=~ - \frac{\partial^2}{\partial w_j^2} \ln p(\mathbf{w}, \mathbf{V}) - \frac{\partial^2}{\partial w_j^2} \text{loglik}(\mathbf{w}, \mathbf{V}) \nonumber \\ &~=~ s_j + \sum_{i=1}^N{ \mu_i (1 - \mu_i) x_{ij}^2 } \tag{4} \end{align}$

The second derivative of the log-posterior w.r.t. $v_{jk}$ turns out to be a bit more complicated, but still easily computed with a single additional pass through the data:

$\begin{align} A_{jk} = - \frac{\partial^2}{\partial v_{jk}^2} \text{logpost}(\mathbf{w}, \mathbf{V}) &~=~ - \frac{\partial^2}{\partial v_{jk}^2} \ln p(\mathbf{w}, \mathbf{V}) - \frac{\partial^2}{\partial v_{jk}^2} \text{loglik}(\mathbf{w}, \mathbf{V}) \nonumber \\ &~=~ s_{jk} + \sum_{i=1}^N{ \mu_i (1 - \mu_i) \left( \frac{\partial F_\text{FM}(\mathbf{x}_i)}{\partial v_{jk}} \right)^2 } \tag{5} \end{align}$

where

$\begin{equation} \frac{\partial}{\partial v_{jk}} F_\text{FM}(\mathbf{x}_i) ~=~ \left( \sum_{j'=1}^D{ v_{j'k} x_{ij'} } \right) x_{ij} - v_{jk} x_{ij}^2 \end{equation}$

We show the Bayesian Factorization Machines algorithm below. It maintains the following invariant: after processing $t$ batches, the weights are distributed as $w_j \sim \mathcal{N}(m_j^{(t)}, 1/s_j^{(t)})$ and the elements of $\mathbf{V}$ are distributed as $v_{jk} \sim \mathcal{N}(m_{jk}^{(t)}, 1/s_{jk}^{(t)})$, which is an approximation of the true posterior after all the data observed so far. In the algorithm below, we update the means $m_j$, $m_{jk}$ and precisions $s_j$, $s_{jk}$ in place, so we omit the superscripts $(t)$.

Algorithm: Bayesian Factorization Machines

Initialize the prior on each weight $w_j$ with $m_j = 0$, $s_j = \lambda_\mathbf{w}$.
Initialize the prior on each $\mathbf{V}$ element $v_{jk}$ with $m_{jk} = 0$, $s_{jk} = \lambda_\mathbf{V}$.
For each new batch of training data $(\mathbf{x}_i, y_i)$ for $i = 1 .. N$:
- Find $\hat{\mathbf{w}}$, $\hat{\mathbf{V}}$ maximizing equation (3) by numerical optimization.
- Compute $A_j$ for each weight according to equation (4).
- Compute $A_{jk}$ for each element of $\mathbf{V}$ according to equation (5).
- Update the weight distribution: $m_j \gets \hat{w}_j$ and $s_j \gets A_j$.
- Update the $\mathbf{V}$ matrix distribution: $m_{jk} \gets \hat{V}_{jk}$ and $s_{jk} \gets A_{jk}$.

As for the linear kernel, our priors have a natural interpretation. By starting with the priors $w_j \sim \mathcal{N}(0, \lambda_\mathbf{w}^{-1})$ and $v_{jk} \sim \mathcal{N}(0, \lambda_\mathbf{V}^{-1})$, our objective function in equation (3) is exactly the same as for (non-Bayesian) Factorization Machines with L2 regularizers $\lambda_\mathbf{w}$ on $\mathbf{w}$ and $\lambda_\mathbf{V}$ on $\mathbf{V}$.

Final Words

We have implemented Thompson sampling and Bayesian Factorization Machines, and we are testing these methods to efficiently navigate between exploration and exploitation. We can fine-tune the desired amount of exploration by scaling the linear precisions $s_j$ and FM precisions $s_{jk}$ by two respective constants. This might be useful, for example, if we change how much training data we use or how many free parameters are in our model, and we want to preserve a certain amount of exploration. Ultimately, these techniques help us ensure that we are using our customers’ budgets in the most efficient way possible.

I’d like to return to our motivating example and show how Thompson sampling works in such a scenario. We evaluate two candidate ads, showing their non-Thompson conversion probability in red, and a histogram of 10,000 Thompson-sampled conversion probabilities in blue.

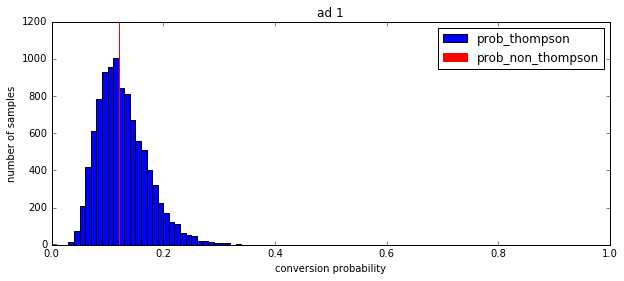
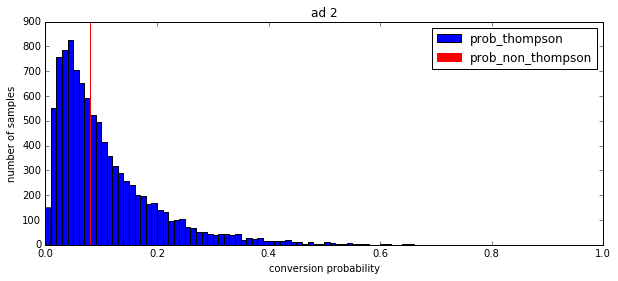
hll-perf

The predicted conversion rate is 0.120 for the first ad and 0.080 for the second ad. So a system with no exploration would always pick the first ad. But the Thompson samples show that there is a lot more uncertainty about the conversion rate of the second ad. (The standard deviation is 0.045 for the first ad and 0.093 for the second ad.) This means that Thompson sampling will pick the second ad some fraction of the time, thus performing exploration. Once the variances shrink enough that the choice of best ad is unambiguous, Thompson sampling will automatically start exploiting that ad.

This has been a really fun project, and the combination of math and engineering involved is a good illustration of the type of work that we do on the Data Science Engineering team. If this piques your interest, check out our open positions!

NextRoll